Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau?...

Câu hỏi:

11/12/2024 11.4 K

A. vô số.

Đáp án chủ yếu xác

B. 3

C. 2

D. 1

Đáp án A

Gọi hai tuyến phố trực tiếp chéo cánh nhau là a và b, c là đường thẳng liền mạch tuy nhiên song với a và rời b.

Gọi mặt mày phẳng $(α) \equiv (b, c) .$ Do $a // c \Rightarrow a // (α) .$

Giả sử mặt mày phẳng lặng $(β) // (α)$ mà $b \subset (α) \Rightarrow b // (β) .$

Mặt không giống $a // (α) \Rightarrow a // (β) .$ Có vô số mặt mày phẳng lặng $(β) // (α) .$

Nên với vô số mặt mày phẳng lặng tuy nhiên song đối với tất cả hai tuyến phố trực tiếp chéo cánh nhau.

Lý thuyết Hai mặt mày phẳng lặng tuy nhiên song

1. Hai mặt mày phẳng lặng tuy nhiên song

Hai mặt $(α)$ và $(β)$ được gọi là tuy nhiên song cùng nhau nếu như bọn chúng không tồn tại điểm công cộng. Kí hiệu $(α)$ // $(β)$ hay $(β)$ // $(α)$ .

(ảnh 1)

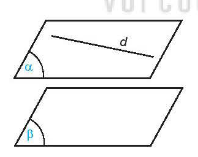
*Nhận xét: ${\begin{cases} (α) / / (β) \\ d \subset (α) \end{cases} \Rightarrow d / / (β)$ .

2. Điều khiếu nại và đặc thù của nhì mặt mày phẳng lặng tuy nhiên song

Nếu mặt mày phẳng $(α)$ chứa hai tuyến phố trực tiếp rời nhau và hai tuyến phố trực tiếp này tuy nhiên song với mặt mày phẳng lặng phẳng $(β)$ thì $(α)$ và $(β)$ song tuy nhiên cùng nhau.

(ảnh 2)

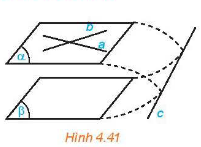
Qua một điểm ở ngoài một phía phẳng lặng cho tới trước với cùng một và có một mặt mày phẳng lặng tuy nhiên song với mặt mày phẳng lặng tiếp tục cho tới.

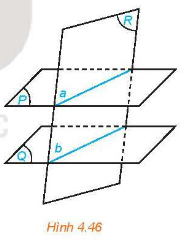
Cho nhì mặt mày phẳng lặng tuy nhiên tuy nhiên. Nếu một phía phẳng lặng rời mặt mày phẳng lặng này thì cũng rời mặt mày phẳng lặng cơ và nhì gửi gắm tuyến tuy nhiên song cùng nhau.

(ảnh 3)

Xem thêm thắt một trong những kỹ năng và kiến thức liên quan:

Lý thuyết Hai mặt mày phẳng lặng tuy nhiên song (Kết nối tri thức) hoặc, cụ thể | Toán lớp 11

50 Bài luyện Hai mặt mày phẳng lặng tuy nhiên song (có đáp án)- Toán 11

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho hình chóp S.ABCD với lòng ABCD là hình bình hành tâm O. Gọi M, N theo thứ tự là trung điểm của SA và SD. Trong những xác minh sau, xác minh nào là sai?

Câu 2:

Cho hình chóp S.ABCD với lòng ABCD là hình bình hành. Gọi M, N, Phường theo thứ tự là trung điểm SA, SB, SC.

a) Chứng minh (MNP) // (ABCD)

Câu 3:

Cho hình chóp S.ABCD với lòng ABCD là hình bình hành tâm O. Gọi M, N theo thứ tự là trung điểm của những cạnh SA, SD.

a) Chứng minh rằng (OMN) tuy nhiên song với (SBC)

Câu 4:

Hãy lựa chọn xác minh sai.

Câu 5:

Cho hình lập phương ABCD.A'B'C'D', với M, N, Phường theo thứ tự là trung điểm của những cạnh AD, DC, DD'. Chứng minh rằng (MNP) tuy nhiên song với (ACD')

Câu 6:

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N theo thứ tự là trung điểm của A'B' và AB. Chứng minh (AMC') // (CNB')

Câu 7:

Cho hình chóp S.ABCD với lòng ABCD là hình bình hành. Gọi I, J, K, L lần lượt là trung điểm của SA, SB, SC, SD. Mệnh đề nào là tại đây đúng?

Câu 8:

Cho tứ diện ABCD với M, N, P theo thứ tự là trọng tâm của $Δ A B C, Δ A C D, Δ A B D .$

Chứng minh rằng $(M N P) // (B C D) .$

Câu 9:

Cho lăng trụ ABC.A'B'C' xuất hiện mặt mày là những hình chữ nhật. Gọi D' là trung điểm của A'B' Lúc cơ CB' tuy nhiên song với

Câu 10:

b) Gọi Q là gửi gắm điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.

Câu 11:

Cho nhì hình bình hành ABCD và ABEF nằm trong nhì mặt mày phẳng lặng phân biệt. Kết trái khoáy nào là tại đây đúng?

Câu 12:

b) Gọi K là trung điểm OM. Chứng minh NK // (SBC)

Câu 13:

Cho nhì hình vuông vắn ABCD và ABEF ở nhập nhì mặt mày phẳng lặng phân biệt. Trên những lối chéo cánh AC và BF theo thứ tự lấy những điểm M, N sao cho tới AM = BN. Các đường thẳng liền mạch tuy nhiên song với AB vẽ kể từ M, N theo thứ tự rời AD và AF bên trên M' và N'.

a) (ADF) // (BCE)

Câu 14:

b) (DEF) // (MM'N'N)