Đường Trung Tuyến Trong Tam Giác Đều Cạnh a: Khám Phá Hình Học Kỳ Diệu

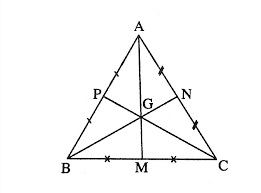
Đường trung tuyến vô tam giác đều là 1 trong định nghĩa cần thiết vô hình học tập, tương quan cho tới đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Đối với tam giác đều, từng lối trung tuyến đều phải sở hữu đặc điểm quan trọng đặc biệt sau:

Tính Chất

• Mỗi lối trung tuyến cũng chính là lối cao, lối phân giác và lối trung trực của cạnh cơ.
• Ba lối trung tuyến vô tam giác đều phải sở hữu chừng nhiều năm cân nhau.
• Các lối trung tuyến bắt gặp nhau bên trên trọng tâm, phân chia từng lối trung tuyến trở nên tỷ trọng 2:1, với nút giao nhau ở cơ hội đỉnh gấp rất nhiều lần khoảng cách cho tới trung điểm cạnh.
• Ba lối trung tuyến phân chia tam giác trở nên sáu tam giác nhỏ sở hữu diện tích S cân nhau.

Công Thức Tính Độ Dài Đường Trung Tuyến

Độ nhiều năm lối trung tuyến \( m \) vô tam giác đều với cạnh có tính nhiều năm \( a \) được xem bởi vì công thức:

\[
m = \frac{\sqrt{3}}{2} a
\]

Đây là công thức đặc biệt hữu ích trong những việc đo lường và tính toán những việc tương quan cho tới tam giác đều, quan trọng đặc biệt Khi tất cả chúng ta cần thiết xác lập khoảng cách kể từ trọng tâm cho tới những đỉnh hoặc những cạnh của tam giác.

Ví Dụ Minh Họa

Xét tam giác đều \( ABC \) với cạnh \( a = 6 \, \text{cm} \), chừng nhiều năm lối trung tuyến \( AM \) tiếp tục là:

\[
AM = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \, \text{cm}
\]

Điều này đã cho thấy rằng lối trung tuyến không những tương quan cho tới cấu tạo hình học tập của tam giác tuy nhiên còn tồn tại tầm quan trọng cần thiết trong những việc đo lường và tính toán và vận dụng vô thực tiễn đưa.

Đường trung tuyến vô tam giác đều là đoạn trực tiếp nối từ 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trong một tam giác đều, phụ thân lối trung tuyến sở hữu Điểm sáng nổi trội là bọn chúng đều phải sở hữu chừng nhiều năm cân nhau và hạn chế nhau bên trên trọng tâm của tam giác, là vấn đề cơ hội từng đỉnh một khoảng chừng bởi vì nhị phần phụ thân chừng nhiều năm từng lối trung tuyến.

• Mỗi lối trung tuyến phân chia tam giác trở nên nhị tam giác nhỏ sở hữu diện tích S cân nhau.
• Điểm kí thác nhau của phụ thân lối trung tuyến là trọng tâm của tam giác, đặc điểm đó cũng chính là tâm của lối tròn xoe nội tiếp tam giác.

Tính hóa học hình học tập quan trọng đặc biệt này thực hiện mang đến lối trung tuyến vô tam giác đều không những là 1 trong định nghĩa cơ bạn dạng mà còn phải là 1 trong khí cụ cần thiết trong số việc hình học tập phẳng phiu. Đường trung tuyến không những chung xác lập trọng tâm tuy nhiên còn là một khóa xe nhằm giải quyết và xử lý nhiều yếu tố tương quan cho tới tính đối xứng và cân đối vô hình học tập.

Đường trung tuyến vô tam giác đều là đường thẳng liền mạch nối từ 1 đỉnh cho tới trung điểm của cạnh đối lập. Đường trung tuyến này còn có những đặc điểm quan trọng đặc biệt và cần thiết vô hình học tập, như sau:

• Độ nhiều năm của lối trung tuyến bởi vì 1/2 chừng nhiều năm cạnh ứng của tam giác, phân chia tam giác trở nên nhị tam giác nhỏ sở hữu diện tích S cân nhau.
• Mỗi lối trung tuyến vô tam giác đều còn là một lối cao và lối phân giác của tam giác cơ, phản ánh tính đối xứng tuyệt vời nhất của tam giác đều qua loa từng góc và từng cạnh.
• Ba lối trung tuyến vô tam giác đều hạn chế nhau bên trên một điểm độc nhất gọi là trọng tâm, là vấn đề cân đối toàn bộ những nhân tố hình học tập của tam giác và cũng chính là tâm của lối tròn xoe nội tiếp tam giác cơ.

Ứng dụng của những lối trung tuyến không những số lượng giới hạn vô lý thuyết, bọn chúng còn đặc biệt hữu ích trong những việc giải những việc thực tiễn như phân loại khu đất đai, xác xác định trí trọng tâm vô chuyên môn, hoặc trong số việc về đo lường và kiến thiết. Chính chính vì vậy, việc nắm rõ những đặc điểm này sẽ hỗ trợ ích thật nhiều vô học hành và phần mềm thực tiễn.

Đường trung tuyến vô tam giác đều phải sở hữu nhiều phần mềm cần thiết không những vô lý thuyết hình học tập mà còn phải trong tương đối nhiều nghành nghề không giống của cuộc sống và technology. Dưới đó là một vài phần mềm thực tiễn của lối trung tuyến:

• Phân phân chia khu đất đai: Đường trung tuyến chung phân loại diện tích S của tam giác trở nên sáu tam giác nhỏ sở hữu diện tích S cân nhau, đặc biệt hữu ích trong số việc phân loại gia tài hoặc khu đất đai.
• Kỹ thuật và thiết kế: Trong nghành nghề chuyên môn, lối trung tuyến chung xác lập trọng tâm của những cấu tạo, tương hỗ vô kiến thiết những thành phần công cụ sở hữu tính đối xứng cao và vô kiến thiết hình đồ họa muốn tạo đi ra những kiến thiết cân đối và hợp lý về mặt mũi thẩm mỹ và làm đẹp.
• Giáo dục: Đường trung tuyến được dùng như 1 khí cụ giảng dạy dỗ hữu ích nhằm lý giải những định nghĩa hình học tập trực quan lại, chung học viên đơn giản tưởng tượng và hiểu bài xích rộng lớn.
• Công nghệ thông tin: Các thuật toán tương quan cho tới lối trung tuyến được phần mềm vô xử lý hình hình họa và tối ưu hóa mạng, chung nâng cấp hiệu suất cao và chừng đúng mực của những khối hệ thống technology vấn đề.
• Đo đạc địa lý: Đường trung tuyến cũng rất được dùng vô đo lường địa lý nhằm xác xác định trí trung tâm của những điểm, hữu ích trong những việc lập bạn dạng thiết bị và quy hướng khu đô thị.

Các phần mềm này chỉ là 1 trong phần vô số nhiều kĩ năng phần mềm của lối trung tuyến, đã cho thấy vai trò của chính nó trong tương đối nhiều nghành nghề không giống nhau.

Lịch sử cải tiến và phát triển những cách thức tính lối trung tuyến vô tam giác đều tiếp tục chính thức kể từ thời cổ truyền. Các căn nhà toán học tập như Euclid tiếp tục nói đến những đặc điểm và công thức của lối trung tuyến trong số kiệt tác của tớ.

• Thời cổ đại: Euclid, vô kiệt tác "Các nguyên vẹn lý", đã lấy đi ra những tìm hiểu lúc đầu về lối trung tuyến, minh chứng bọn chúng như là 1 trong phần luôn luôn phải có vô hình học tập Euclid.
• Thời Trung cổ: Các căn nhà toán học tập Ả Rập và châu Âu tiếp tục cải tiến và phát triển và không ngừng mở rộng những kỹ năng của Euclid, vận dụng những cách thức tính lối trung tuyến vô những việc kiến thiết phong cách thiết kế và thiên văn học tập.
• Thời kỳ Phục hưng: Với sự cải tiến và phát triển của hình học tập phân tách, những căn nhà toán học tập như René Descartes tiếp tục không ngừng mở rộng nắm vững về lối trung tuyến, link bọn chúng với những định nghĩa mới nhất vô toán học tập.

Quá trình này đã cho thấy sự kết nối quan trọng thân mật lối trung tuyến và sự cải tiến và phát triển của toán học tập qua loa những thời kỳ, kể từ giản dị và đơn giản cho tới phức tạp, và phần mềm của chính nó trong số nghành nghề không giống nhau của khoa học tập và chuyên môn.

Xét một ví dụ ví dụ về tính chất lối trung tuyến vô tam giác đều nhằm làm rõ rộng lớn cơ hội vận dụng công thức và trí tuệ về đặc điểm hình học tập của chính nó. Dưới đó là việc và cơ hội giải:

1. Cho tam giác đều ABC sở hữu cạnh bởi vì 6 centimet. Cần tính chừng nhiều năm lối trung tuyến kể từ đỉnh A xuống cạnh BC.
2. Sử dụng công thức lối trung tuyến mang đến tam giác đều: \( m = \frac{\sqrt{3}}{2} \times a \)
3. Thay số vô công thức: \( a = 6 \) centimet, tớ sở hữu \( m = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \text{ cm} \approx 5.196 \text{ cm} \)

Kết quả: Độ nhiều năm lối trung tuyến kể từ đỉnh A cho tới cạnh BC là khoảng chừng 5.196 centimet.

Điều này minh họa phương pháp tính giản dị và đơn giản tuy nhiên đúng mực, được chấp nhận hiểu sâu sắc về cấu tạo và đo lường và tính toán vô hình học tập tam giác đều.

Dưới đó là một vài mối cung cấp khoáng sản hữu ích nhằm lần hiểu sâu sắc rộng lớn về lối trung tuyến vô tam giác đều và những định nghĩa liên quan:

• Math Open Reference: Cung cung cấp chỉ dẫn cụ thể về phong thái vẽ lối trung tuyến của một tam giác, bao hàm cả những bài xích tập luyện thực hành thực tế rất có thể in đi ra nhằm rèn luyện. Xem thêm thắt bên trên Math Open Reference nhằm tìm hiểu những cách thức không giống nhau vô hình học tập.
• Brilliant.org: Một trang web dạy dỗ cung ứng vấn đề cụ thể về những đặc điểm của tam giác đều, bao hàm cả công thức tính diện tích S và chu vi. Brilliant.org cũng lý giải cơ hội những lối cao, trung tuyến và phân giác của tam giác túc tắc trùng nhau.
• Byju's: Cung cung cấp những ví dụ giải quyết và xử lý và lý thuyết về tam giác đều, bao hàm cả công thức diện tích S và chu vi, cũng giống như những việc tương quan cho tới lối trung tuyến. Byju's là 1 trong mối cung cấp khoáng sản ấn tượng nhằm hiểu sâu sắc rộng lớn về cấu tạo và đo lường và tính toán của tam giác đều.
• Khan Academy: Cung cung cấp những bài xích giảng đoạn phim và bài xích tập luyện tương tác nhằm lý giải những định nghĩa hình học tập cơ bạn dạng và nâng lên, bao hàm cả lối trung tuyến và những trung tâm tam giác không giống nhau như trọng tâm và tâm lối tròn xoe nước ngoài tiếp.

Những mối cung cấp này không những chung gia tăng kỹ năng cơ bạn dạng về tam giác mà còn phải cung ứng những khí cụ hữu ích nhằm phân tách và giải quyết và xử lý những việc phức tạp rộng lớn tương quan cho tới hình học tập.