Lý thuyết Hai đường thẳng chéo nhau và nhì đường thẳng tuy vậy song lớp 11 bao gồm lý thuyết cụ thể, ngắn ngủi gọn gàng và bài xích tập dượt tự động luyện với điều giải cụ thể sẽ hỗ trợ học viên nắm rõ kiến thức và kỹ năng trọng tâm Toán 11 Bài 2: Hai đường thẳng chéo nhau và nhì đường thẳng tuy vậy tuy vậy.
Lý thuyết Toán 11 Bài 2: Hai đường thẳng chéo nhau và nhì đường thẳng tuy vậy song
Bài giảng Toán 11 Bài 2: Hai đường thẳng chéo nhau và nhì đường thẳng tuy vậy song
A. Lý thuyết
I. Vị trí kha khá của hai tuyến phố trực tiếp nhập không khí.
Cho hai tuyến phố trực tiếp a và b nhập không khí. Khi tê liệt rất có thể xẩy ra một trong những tình huống sau:
- Trường phù hợp 1. Có một phía phẳng lặng chứa chấp a và b.
Khi tê liệt, tao phát biểu a và b đồng phẳng lặng. Theo sản phẩm của hình học tập phẳng lặng với 3 năng lực xảy ra:
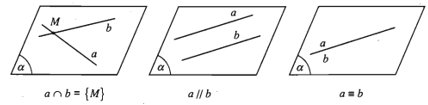
i) a và b với điểm cộng đồng có một không hai M. Ta phát biểu a và b cắt nhau bên trên M và kí hiệu . Ta rất có thể ghi chép .
ii) a và b không tồn tại điểm cộng đồng. Ta phát biểu a và b song tuy vậy với nhau và kí hiệu là a // b.
iii) a trùng b, kí hiệu là .
- Trường phù hợp 2. Không xuất hiện phẳng lặng này chứa chấp a và b.
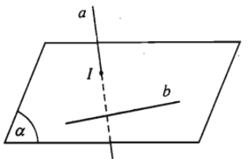
Khi tê liệt tao phát biểu a và b chéo nhau hoặc a chéo với b.
- Ví dụ 1. Cho tứ diện ABCD. Hãy đã cho thấy những cặp đường thẳng liền mạch chéo cánh nhau.
Lời giải:
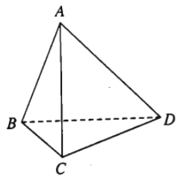
Đường trực tiếp AB và CD chéo cánh nhau.
Đường trực tiếp AC và BD chéo cánh nhau.
Đường trực tiếp AD và BC chéo cánh nhau.
II. Tính chất
- Định lí. Trong không khí, qua chuyện một điểm ko phía trên đường thẳng liền mạch cho tới trước, với cùng 1 và duy nhất đường thẳng liền mạch tuy vậy song với đường thẳng liền mạch tiếp tục cho tới.
- Định lí (về uỷ thác tuyến của phụ vương mặt mũi phẳng).
Nếu phụ vương mặt mũi phẳng lặng song một hạn chế nhau theo gót phụ vương uỷ thác tuyến phân biệt thì phụ vương uỷ thác tuyến ấy hoặc đồng quy hoặc song một tuy vậy song cùng nhau.
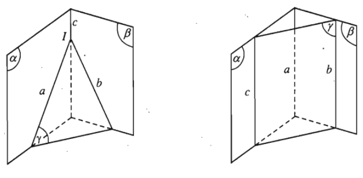
- Hệ quả. Nếu nhì mặt mũi phẳng lặng phân biệt theo thứ tự chứa chấp hai tuyến phố trực tiếp tuy vậy song thì uỷ thác tuyến của bọn chúng (nếu có) cũng tuy vậy song với hai tuyến phố trực tiếp tê liệt hoặc trùng với 1 trong các hai tuyến phố trực tiếp tê liệt.
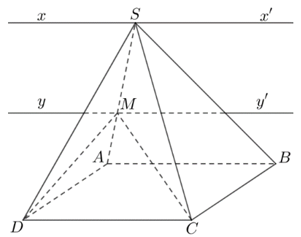
Ví dụ 2. Cho hình chóp S.ABCD với lòng ABCD là hình bình hành. Tìm uỷ thác tuyến của những mặt mũi phẳng:
a) (SAD) và (SBC).
b) (MCD) và (SAB), với M là 1 trong những điểm bất kì nằm trong cạnh SA.
Lời giải:
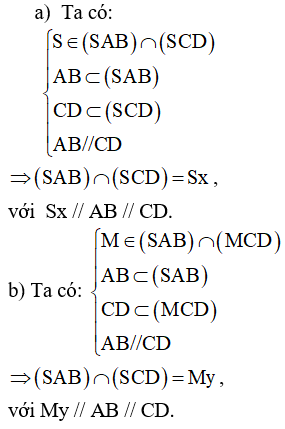
- Định lí. Hai đường thẳng liền mạch phân biệt nằm trong tuy vậy song với đường thẳng liền mạch loại phụ vương thì tuy vậy song cùng nhau.
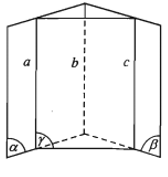
Ta có: a // c; b // c nên a // b hoặc a // b // c (ba đường thẳng liền mạch tuy vậy song).
Ví dụ 3. Cho hình chóp S.ABCD với lòng ABCD là hình bình hành. Gọi I, J theo thứ tự là trung điểm của những cạnh SA, SB. Chứng minh rằng IJ // AB, kể từ tê liệt suy rời khỏi IJ // CD.
Lời giải:
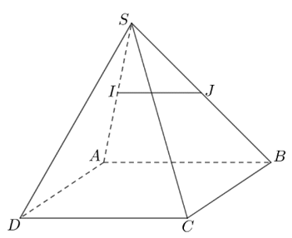
Xét tam giác SAB với I, J theo thứ tự là trung điểm của những cạnh SA, SB nên IJ là lối tầm của tam giác SAB.
Từ tê liệt suy rời khỏi IJ // AB.
Lại với AB // CD (vì ABCD là hình bình hành) nên kể từ tê liệt tao với IJ // CD (vì nằm trong tuy vậy song với đường thẳng liền mạch AB).
B. Bài tập dượt tự động luyện
Bài 1. Cho tứ diện ABCD. Chứng minh rằng AB và CD là hai tuyến phố trực tiếp chéo cánh nhau.
Lời giải:
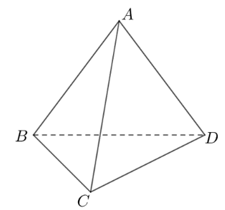
Giả sử AB và CD ko chéo cánh nhau, tức thị hai tuyến phố trực tiếp này đồng phẳng lặng.
Khi tê liệt AB và CD rất có thể tuy vậy song cùng nhau hoặc hạn chế nhau bên trên một điểm hoặc trùng nhau (vô lý vì thế ABCD là tứ diện nên 4 điểm A, B, C, D ko đồng phẳng).
Vậy AB và CD chéo cánh nhau.
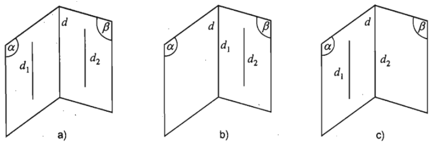
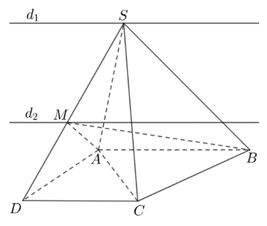
Bài 2. Cho hình chóp S.ABCD với lòng ABCD là hình thang, lòng rộng lớn AB. Gọi M là vấn đề bất kì nằm trong đoạn trực tiếp SD. Tìm uỷ thác tuyến của những mặt mũi phẳng:
a) .
b) . Từ tê liệt chứng tỏ d1 // d2.
Lời giải:
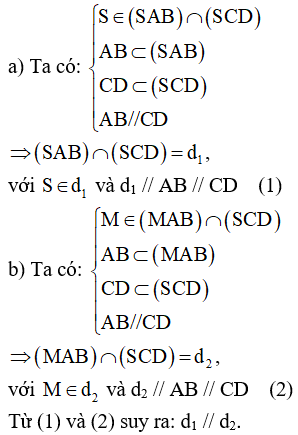
Bài 3. Cho tứ diện ABCD. Gọi M, N theo thứ tự là những điểm với những cạnh AB, AC sao cho tới ; I, J theo thứ tự là trung điểm của BD, CD.
a) Chứng minh rằng MN // BC.
b) Tứ giác MNJI là hình gì.
Lời giải:
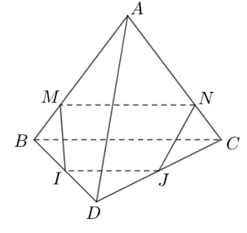
a) Xét mp(ABC) có:
, kể từ tê liệt suy rời khỏi MN // BC (1) (Định lý Ta-lét đảo).
b) Xét mp(BCD) có: I, J theo thứ tự là trung điểm của BD, CD
Nên IJ là lối tầm của tam giác BCD.
Từ tê liệt suy rời khỏi IJ // BC (2).
Từ (1) và (2) suy rời khỏi MN // IJ.
Vậy tứ giác MNJI là hình thang.
Bài 4. Cho hình chóp S.ABCD với lòng ABCD là hình bình hành tâm O. Gọi M là trung điểm của SA. Tìm tiết diện của mặt mũi phẳng lặng (P) với hình chóp S.ABCD, biết (P) là mặt mũi phẳng lặng qua chuyện điểm M và tuy vậy song với SC, AD.
Lời giải:
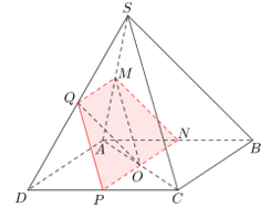
Qua M kẻ đường thẳng liền mạch MQ // AD với Q nằm trong SD.
Có MO // SC (do MO là lối tầm của tam giác SAC).
Trong mp(ABCD), qua chuyện O dựng đường thẳng liền mạch tuy vậy song với AD hạn chế AB, CD theo thứ tự bên trên N và P..
Từ tê liệt tao có:
Vậy tiết diện tạo nên vì chưng (P) và hình chóp là hình thang MNPQ.
Trắc nghiệm Toán 11 Bài 2: Hai đường thẳng liền mạch chéo cánh nhau và hai tuyến phố trực tiếp tuy vậy song
Câu 1: Trong những mệnh đề sau, mệnh đề này đúng?
A. Hai đường thẳng liền mạch chéo cánh nhau Lúc bọn chúng không tồn tại điểm cộng đồng.
B. Hai đường thẳng liền mạch không tồn tại điểm cộng đồng là hai tuyến phố trực tiếp tuy vậy song hoặc chéo cánh nhau.
C. Hai đường thẳng liền mạch tuy vậy song nhau Lúc bọn chúng phía trên và một mặt mũi phẳng lặng.
D. Khi hai tuyến phố trực tiếp phía trên nhì mặt mũi phẳng lặng thì hai tuyến phố trực tiếp tê liệt chéo cánh nhau.
Đáp án: B
Giải thích:
Dựa nhập địa điểm kha khá đằm thắm hai tuyến phố trực tiếp.
Câu 2: Trong những mệnh đề sau, mệnh đề này đúng?
A. Hai đường thẳng liền mạch theo thứ tự phía trên nhì mặt mũi phẳng lặng phân biệt thì chéo cánh nhau.
B. Hai đường thẳng liền mạch không tồn tại điểm cộng đồng thì chéo cánh nhau.
C. Hai đường thẳng liền mạch chéo cánh nhau thì không tồn tại điểm cộng đồng.
D. Hai đường thẳng liền mạch phân biệt ko tuy vậy song thì chéo cánh nhau.
Đáp án: C
Câu 3: Cho hình chóp S.ABCD. Gọi M, N, P.., Q, R, T theo thứ tự là trung điểm AC, BD, BC, CD, SA, SD. Bốn điểm này tại đây đồng phẳng?
A.
B.
C.
D.
Đáp án: B
Giải thích:
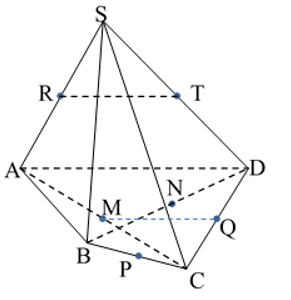
Ta với RT là lối tầm của tam giác SAD nên .
MQ là lối tầm của tam giác ACD nên .
Suy rời khỏi . Do tê liệt M , Q , R ,T đồng phẳng lặng.
Câu 4: Chọn mệnh đề trúng trong những mệnh đề sau:
A. Hai đường thẳng liền mạch không tồn tại điểm cộng đồng thì chéo cánh nhau.
B. Hai đường thẳng liền mạch phân biệt không tồn tại điểm cộng đồng thì chéo cánh nhau.
C. Hai đường thẳng liền mạch chéo cánh nhau thì không tồn tại điểm cộng đồng.
D. Hai đường thẳng liền mạch theo thứ tự phía trên nhì mặt mũi phẳng lặng phân biệt thì chéo cánh nhau.
Đáp án: C
Giải thích:
Câu A sai vì thế hai tuyến phố trực tiếp không tồn tại điểm cộng đồng thì chéo cánh nhau hoặc tuy vậy song cùng nhau.
Câu B sai vì thế hai tuyến phố trực tiếp phân biệt không tồn tại điểm cộng đồng thì chéo cánh nhau hoặc tuy vậy song cùng nhau.
Câu D sai vì thế hai tuyến phố trực tiếp phân biệt phía trên nhì mặt mũi phẳng lặng phân biệt thì rất có thể chéo cánh nhau hoặc tuy vậy song cùng nhau.
Câu 5: Hãy Chọn Câu đúng?
A. Hai đường thẳng liền mạch nằm trong tuy vậy song với cùng 1 đường thẳng liền mạch loại phụ vương thì tuy vậy song cùng nhau.
B. Hai đường thẳng liền mạch tuy vậy song nhau nếu như bọn chúng không tồn tại điểm cộng đồng.
C. Hai đường thẳng liền mạch nằm trong tuy vậy song với một phía phẳng lặng thì tuy vậy song cùng nhau.
D. Không xuất hiện phẳng lặng này chứa chấp cả hai tuyến phố trực tiếp a và b thì tao phát biểu a và b chéo cánh nhau.
Đáp án: D
Giải thích:
- Hai đường thẳng liền mạch nằm trong tuy vậy song với cùng 1 đường thẳng liền mạch loại phụ vương thì rất có thể trùng nhauA sai.
- Hai đường thẳng liền mạch không tồn tại điểm cộng đồng thì tuy vậy song hoặc chéo cánh nhauB sai.
- Hai đường thẳng liền mạch nằm trong tuy vậy song với một phía phẳng lặng thì rất có thể hạn chế, trùng hoặc chéo cánh nhauC sai.
- Hai đường thẳng liền mạch chéo cánh nhau nếu như bọn chúng ko đồng phẳngD đúng.
Câu 6: Hãy Chọn Câu đúng?
A. Nếu phụ vương mặt mũi phẳng lặng hạn chế nhau theo gót phụ vương uỷ thác tuyến thì phụ vương uỷ thác tuyến tê liệt đồng qui.
B. Nếu nhì mặt mũi phẳng lặng theo thứ tự chứa chấp hai tuyến phố trực tiếp tuy vậy song thì uỷ thác tuyến, nếu như với, của bọn chúng tiếp tục tuy vậy song đối với tất cả hai tuyến phố trực tiếp tê liệt.
C. Nếu hai tuyến phố trực tiếp a và b chéo cánh nhau thì với hai tuyến phố trực tiếp p và q tuy vậy song nhau tuy nhiên từng lối đều hạn chế cả a và b.
D. Hai đường thẳng liền mạch phân biệt nằm trong tuỳ thuộc một phía phẳng lặng thì ko chéo cánh nhau.
Đáp án: D
Giải thích:
- Nếu phụ vương mặt mũi phẳng lặng hạn chế nhau theo gót phụ vương uỷ thác tuyến phân biệt thì rất có thể song một tuy vậy song nhauA sai.
- Nếu nhì mặt mũi phẳng lặng theo thứ tự chứa chấp hai tuyến phố trực tiếp tuy vậy song thì uỷ thác tuyến, nếu như với, của bọn chúng rất có thể trùng với 1 trong các hai tuyến phố trực tiếp đóB sai.
- Giả sử: p hạn chế a và b theo thứ tự bên trên A và B . q hạn chế a và b theo thứ tự bên trên và .
Nếu đồng phẳng lặng đồng phẳng lặng ( mâu thuẫn)C sai.
- Hai đường thẳng liền mạch chéo cánh nhau nếu như bọn chúng ko đồng phẳngD đúng.
Câu 7: Cho hình chóp S.ABCD với lòng là hình bình hành. Gọi I, J, E, F theo thứ tự là trung điểm SA, SB, SC, SD. Trong những đường thẳng liền mạch sau, đường thẳng liền mạch này không tuy vậy song với ?
A. EF
B. DC
C. AD
D. AB
Đáp án: C
Giải thích:
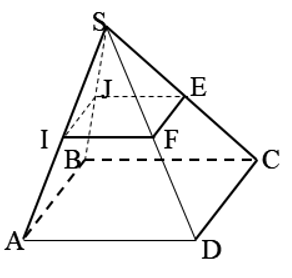
Ta với IJ là lối tầm tam giác SAB nên .
D. đúng.
ABCD là hình bình hành nên . Suy rời khỏi . B. đúng.
EF là lối tầm tam giác SCD nên . Suy rời khỏi . A. đúng.
Do tê liệt lựa chọn đáp án C.
Câu 8: Cho hai tuyến phố trực tiếp phân biệt a và b nằm trong tuỳ thuộc mp.
Có từng nào địa điểm kha khá đằm thắm a và b?
A. 1.
B. 2.
C. 3.
D. 4.
Đáp án: C
Giải thích:
Vị trí kha khá của hai tuyến phố trực tiếp nằm trong ở trong một mặt mũi phẳng lặng là:
+ Hai đường thẳng liền mạch trùng nhau.
+ Hai đường thẳng liền mạch hạn chế nhau.
+ Hai đường thẳng liền mạch tuy vậy tuy vậy.
Câu 9: Cho hai tuyến phố trực tiếp chéo cánh nhau a và b. Lấy A,B nằm trong a và C, D nằm trong b. Khẳng lăm le này tại đây đúng Lúc nói tới hai tuyến phố trực tiếp AD và BC?
A. Có thể tuy vậy song hoặc hạn chế nhau.
B. Cắt nhau.
C. Song tuy vậy nhau.
D. Chéo nhau.
Đáp án: D
Giải thích:
Ta với a và b chéo cánh nhau nên A, B, C, D ko đồng phẳng lặng. Do tê liệt AD và BC chéo cánh nhau.
Câu 10: Cho hình chóp S.ABCD với lòng ABCD là hình bình hành. Gọi d là uỷ thác tuyến của nhì mặt mũi phẳng lặng và . Khẳng lăm le này tại đây đúng?
A. d qua chuyện S và tuy vậy song với BC.
B. d qua chuyện S và tuy vậy song với DC.
C. d qua chuyện S và tuy vậy song với AB.
D. d qua chuyện S và tuy vậy song với BD.
Đáp án: A
Giải thích:
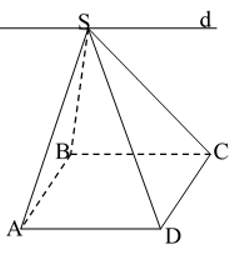
Ta với
(Theo hệ trái ngược của lăm le lý 2 (Giao tuyến của phụ vương mặt mũi phẳng)).
Xem tăng những bài xích tổng hợp lý và phải chăng thuyết Toán lớp 11 rất đầy đủ, cụ thể khác:
Lý thuyết Đường thẳng và mặt phẳng tuy vậy song
Lý thuyết Hai mặt phẳng tuy vậy song
Lý thuyết Phép chiếu tuy vậy tuy vậy. Hình biểu diễn của một hình ko gian
Lý thuyết Ôn tập dượt chương 2
Lý thuyết Vectơ nhập ko gian
