Tính thể tích hình vỏ hộp chữ nhật sở hữu chiều lâu năm a, chiều rộng lớn b, độ cao c. a) a = 5cm; b = 4cm; c = 9cm. b) a = 1,5m; b = 1,1m; c = 0,5m.
Lựa lựa chọn câu nhằm coi lời nói giải nhanh chóng hơn
Bài 1
Video chỉ dẫn giải
Tính thể tích hình vỏ hộp chữ nhật sở hữu chiều lâu năm a, chiều rộng lớn b, độ cao c.
a) a = 5cm; b = 4cm; c = 9cm.
b) a = 1,5m; b = 1,1m; c = 0,5m.
c) a = \(\dfrac{2}{5}\)dm; b = \(\dfrac{1}{3}\)dm; c = \(\dfrac{3}{4}\)dm.
Phương pháp giải:
Muốn tính thể tích hình vỏ hộp chữ nhật tớ lấy chiều lâu năm nhân với chiều rộng lớn rồi nhân với độ cao (cùng một đơn vị chức năng đo).
Lời giải chi tiết:
a) Thể tích của hình vỏ hộp chữ nhật cơ là:
V = 5 x 4 x 9 = 180 (cm3)
b) Thể tích của hình vỏ hộp chữ nhật cơ là:
V = 1,5 x 1,1 x 0,5 = 0,825 (m3)
c) Thể tích của hình vỏ hộp chữ nhật cơ là:
V = \(\dfrac{2}{5}\) x \(\dfrac{1}{3}\) x \(\dfrac{3}{4}\) = \(\dfrac{1}{10}\) (dm3)
Bài 2
Video chỉ dẫn giải
Tính thể tích của khối mộc sở hữu dạng như hình bên:
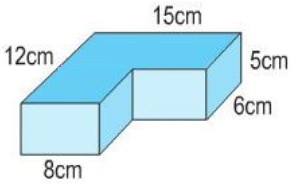
Phương pháp giải:
Chia khối mộc trở thành những hình vỏ hộp chữ nhật nhỏ rồi tính thể tích từng hình theo đuổi công thức V = a x b x c
(a, b, c là tía độ cao thấp của hình vỏ hộp chữ nhật), kể từ cơ suy rời khỏi thể tích khối mộc lúc đầu.
Lời giải chi tiết:
Cách 1 :
Chia khối mộc trở thành nhị hình vỏ hộp chữ nhật A và B như hình bên dưới đây:
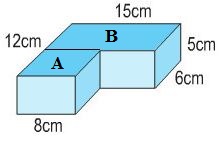
Chiều rộng lớn của hình vỏ hộp chữ nhật A là:
12 - 6 = 6 (cm)
Thể tích hình vỏ hộp chữ nhật A là:
8 × 6 × 5 = 240 (cm3)
Thể tích hình vỏ hộp chữ nhật B là:
15 × 6 × 5 = 450 (cm3)
Thể tích của khối mộc là:
240 + 450 = 690 (cm3)
Đáp số: 690cm3.
Cách 2:
Chia khối mộc trở thành nhị hình vỏ hộp chữ nhật C và D như hình bên dưới đây:
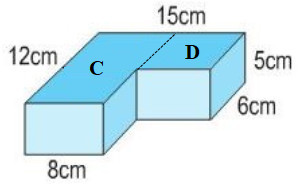
Thể tích hình vỏ hộp chữ nhật C là:
12 × 8 × 5 = 480 (cm3)
Thể tích hình vỏ hộp chữ nhật D là:
(15 – 8) × 6 × 5 = 210 (cm3)
Thể tích của khối mộc là:
480 + 210 = 690 (cm3)
Đáp số: 690cm3.
Cách 3: Xem hình vẽ mặt mày dưới:
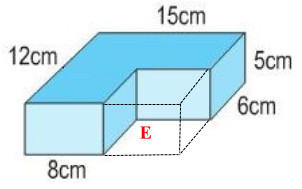
Chiều lâu năm của hình vỏ hộp chữ nhật E là:
15 – 8 = 7 (cm)
Chiều rộng lớn của hình vỏ hộp chữ nhật E là:
12 – 6 = 6 (cm)
Thể tích hình vỏ hộp chữ nhật E là:
7× 6 × 5 = 210 (cm3)
Thể tích của tất cả khối mộc và hình vỏ hộp chữ nhật E là:
15 × 12 × 5 = 900 (cm3)
Thể tích của khối mộc là:
900 – 210 = 690 (cm3)
Đáp số: 690cm3.
Bài 3
Video chỉ dẫn giải
Tính thể tích của hòn đá ở trong bể nước theo như hình bên dưới đây:
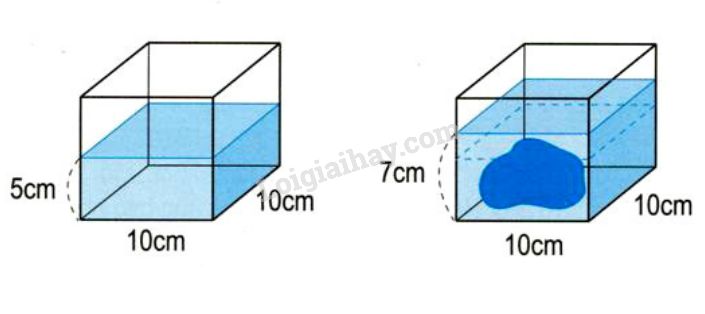
Phương pháp giải:
Cách 1: Thể tích hòn đá = Tổng thể tích hòn đá và nước - thể tích nước nhập bể
Cách 2: Thể tích của hòn đá vị thể tích của hình vỏ hộp chữ nhật (phần nước dưng lên) sở hữu chiều lâu năm 10cm, chiều rộng lớn 10cm và độ cao là: 7 - 5 = 2 (cm).
Lời giải chi tiết:
Cách 1:
Thể tích nước nhập bể là:
10 × 10 × 5 = 500 (cm3)
Tổng thể tích của nước và hòn đá là:
10 × 10 × 7 = 700 (cm3)
Thể tích của hòn đá là:
700 – 500 = 200 (cm3)
Đáp số: 200cm3.
Cách 2:
Chiều cao của phần nước dơ lên là:
7 – 5 = 2 (cm)
Thể tích nước dơ lên là:
10 × 10 × 2 = 200 (cm3)
Thể tích nước dơ lên đó là thể tích hòn đá.
Đáp số: 200cm3.
Lý thuyết
1. Thể tích hình vỏ hộp chữ nhật
Quy tắc: Muốn tính thể tích hình vỏ hộp chữ nhật tớ lấy chiều lâu năm nhân với chiều rộng lớn rồi nhân với độ cao (cùng đơn vị chức năng đo).

Lưu ý: Chiều lâu năm nhân với chiều rộng lớn đó là diện tích S lòng. Vậy hoàn toàn có thể tính thể tích hình vỏ hộp chữ nhật bằng phương pháp lấy diện tích S lòng nhân với độ cao.
Ví dụ: Tính thể tích hình vỏ hộp chữ nhật sở hữu chiều lâu năm \(12cm\), chiều rộng lớn \(5cm\) và độ cao \(8cm\).
Giải:
Thể tích hình vỏ hộp chữ nhật cơ là:
\(12 \times 5 \times 8 = 480\;(c{m^3})\)
Đáp số: \(480c{m^3}\).
2. Một số dạng bài bác tập
Dạng 1: Tính thể tích hình vỏ hộp chữ nhật lúc biết tía kích thước
Phương pháp: Muốn tính thể tích hình vỏ hộp chữ nhật tớ lấy chiều lâu năm nhân với chiều rộng lớn rồi nhân với độ cao (cùng đơn vị chức năng đo).
Dạng 2: Tính độ cao của hình vỏ hộp chữ nhật.
Phương pháp: Chiều cao của hình vỏ hộp chữ nhật phân chia mang đến diện tích S lòng.
\(c = V:(a \times b)\).
Dạng 3: Tính diện tích S lòng lúc biết thể tích
Phương pháp: Diện tích lòng của hình vỏ hộp chữ nhật vị thể tích mang đến cho độ cao.
\(a \times b = V:c\).
Dạng 4: Toán sở hữu lời nói văn (thường tính thể tích nước, độ cao mực nước…)
Phương pháp: Đọc kĩ đề bài bác, xác lập dạng toán và đòi hỏi của đề bài bác rồi giải vấn đề cơ.
Bình luận
![]() Chia sẻ
Chia sẻ
- Toán lớp 5 trang 122, 123 Thể tích hình lập phương
Viết số đo phù hợp nhập dù trống:Một khối kim mô hình lập phương sở hữu cạnh là 0,75m. Mỗi đề-xi-mét khối sắt kẽm kim loại cơ khối lượng 15kg. Hỏi khối sắt kẽm kim loại cơ khối lượng từng nào ki-lô-gam?
- Toán lớp 5 trang 123 Luyện luyện chung
Một hình lập phương sở hữu cạnh 2,5cm. Tính diện tích S một phía, diện tích S toàn phần và thể tích của hình lập phương cơ.
- Toán lớp 5 trang 124, 125 Luyện luyện chung
Bạn Dung tính nhẩm 15% của 120 như sau: 10% của 120 là 12 5% của 120 là 6 Vậy : 15% của 120 là 18. a) Hãy viết lách số phù hợp nhập khu vực chấm nhằm thăm dò 17,5% của 240 theo đuổi phương pháp tính của khách hàng Dung: ... % của 240 là ... ... % của 240 là ... ... % của 240 là ... Vậy : 17,5% của 240 là ... b) Hãy tính 35% của 520 và nêu phương pháp tính.
- Toán lớp 5 trang 126 Giới thiệu hình trụ - Giới thiệu hình cầu
Trong những hình tiếp sau đây sở hữu hình này là hình trụ ? Đồ vật này tiếp sau đây sở hữu hình dáng cầu?
- Toán lớp 5 trang 127 Luyện luyện chung
Cho hình thang vuông ABCD (xem hình vẽ) sở hữu AB = 4cm, DC = 5cm, AD = 3cm. Nối D với B tớ được nhị hình tam giác ABD và BDC. a) Tính diện tích S từng hình tam giác cơ. b) Tính tỉ số Phần Trăm của diện tích S hình tam giác ABD và diện tích S hình tam giác BDC.
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán lớp 5 - Xem ngay lập tức
